Der folgende Text beruht auf Informationen und Auswertungen meines Lesers Dr. Reinhard Seyfarth. Er ist Verfahrenstechniker mit Erfahrung in der Programmierung von statistischen Softwarepaketen.
Der aktuelle Wochenbericht des RKI vom 2.12. könnte in jeder Statistikvorlesung als Beispiel dafür dienen, wie man Informationen verschleiert und schlechte Zahlen schönrechnet.
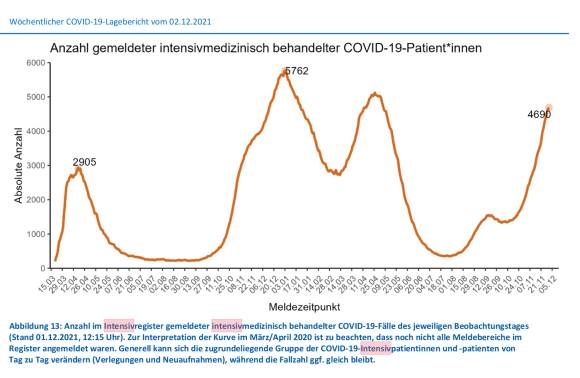
In Abbildung 13 wird die gegenwärtige Belegung der Intensivstationen durch Covid-19-Patienten mit 4690 angegeben. Man sieht dort aber auch, dass der Höchstwert am 03.01.2021 bei 5762 gelegen hat. Gleichzeitig wird nicht erwähnt, dass jetzt aber 4000 Betten weniger zur Verfügung stehen.
Es geht aber noch besser. In der Tabelle 3 des Wochenberichts werden die Mittelwerte der KW 44–47 von auf Intensivstation betreuten symptomatischen COVID-19-Fällen in drei Altersklassen aufgeteilt und nach Impfstatus differenziert. Wenn man die Werte der Altersgruppen zusammenrechnet, kommt man auf bescheidene 1721 Intensivpatienten, also eine sehr große Differenz zur oben angeführten Zahl von 4690 Intensivpatienten.
Letzterer Tageswert ist allerdings vom 01.12.2021 während die nach Alter und Impfstatus aufgeschlüsselten vom Zeitraum 1.11. bis 28.11. stammen. Nimmt man gleichmäßigen Anstieg im Verlauf des November an, müssten zur Mitte des genannten Vierwochenzeitraums etwa 3250 Patienten auf Intensivstationen gelegen haben. Das ist fast doppelt so viel wie die nach Alter und Impfstatus aufgeschlüsselte Summe.
Die Erklärung der Diskrepanz wird in einer Fußnote unter der Tabelle versteckt, wo es heißt: „Alle symptomatischen Fälle, für die aus den übermittelten Angaben hervorgeht, dass sie entweder vollständig geimpft oder ungeimpft waren.“ Wenn man nur von der Hälfte der Intensivpatienten den Impfstatus übermittelt bekommt, ist die Aussagekraft der prominent in der Tabelle herausgestellten Anteilswerte der Geimpften so fragwürdig, dass man die große Unsicherheit der zur Verfügung stehenden Daten unbedingt deutlich benennen sollte. Das Verstecken dieses Makels wirkt unseriös.
Auf S. 21 heißt es in einem anderen Zusammenhang, dass lediglich für 69% der „übermittelten hospitalisierten COVID-19-Fälle ausreichende Angaben zum Impfstatus“ vorliegen. Bei den Covid-Fällen auf Intensivstationen hätte es im Text (und nicht nur versteckt in einer Fußnote) einschränkend heißen müssen, dass nur für rund die Hälfte der Intensivpatienten Angaben zum Impfstatus vorliegen.
Aber so wie es das RKI jetzt hält, ist es immer noch besser als das, was die Behörde vorher tat, nämlich die Patienten mit unbekanntem Impfstatus den nicht Geimpften zuzuschlagen.
Ungeeignete Rechenmethode auf schmaler Informationsbasis
Aber das RKI geht noch einen Schritt weiter. Es berechnet auf dieser schmalen und möglicherweise verzerrten Datenbasis eine Impfeffektivität nach Farrington. (Der Link zur Erläuterung der Methodik im Wochenbericht führt auf eine Seite, die Normalbürgern nicht zugänglich ist.) Ich habe die Formel am Ende dieses Beitrags für Kenner aufgeschrieben.
Die Formel setzt den Anteil der Geimpften an den schwer Erkrankten in Beziehung zum Anteil der Geimpften an der Gesamtbevölkerung. Wenn man diese Formel in kontrollierten klinischen Studien anwendet, ist kaum etwas dagegen zu sagen, da die betrachteten Gruppen gleich groß sein und durch Randomisierung über gleiche statistische Eigenschaften verfügen sollten.
Wendet man die Formel dagegen auf nicht kontrollierte Gruppen aus der realen Welt an, ergeben sich Probleme. Die Gruppengrößen können dann stark voneinander abweichen. Tendenziell sorgt die Formel dafür, dass die Impfeffektivität um so höher wird, je mehr Menschen mit geringem Risiko schwer zu erkranken, geimpft werden.
Impft man nur die Risikogruppen, ist die impfeffektivität geringer als wenn man zusätzlich viele Menschen impft, deren Risiko, schwer zu erkranken, gering ist, ob mit oder ohne Impfung. Denn dann steigt der Anteil der Geimpften an der Bevölkerung, aber der Anteil der Geimpften an allen schwer Erkrankten steigt nicht in gleichem Maße.
Der Leiter der Abteilung Impfprävention der RKI, Ole Wichmann, hat in einem Fachaufsatz aus dem Jahr 2013 ausdrücklich in Sachen Farrington auf die Probleme hingewiesen:
„Die Methode ist aber recht anfällig für Verzerrungen, insbesondere bei sehr niedrigen oder sehr hohen Impfquoten.“
Deshalb erscheint es fragwürdig, die Farrington-Formel so zu verwenden, wie das RKI das tut. Dort, wo die Eigenheiten der Formel die Impfung schlecht aussehen lassen, wendet das RKI sie nicht an. Ein Schelm, wer Böses dabei denkt.
Es zeigt sich nämlich, dass die Formel zu sehr ungünstigen Ergebnissen für die Impfeffektivität neigt, wenn die Impfquote unter 50% liegt. Das RKI schreibt im Wochenbericht über die Altersgruppe der 12 – 17-jährigen mit einer Impfquote von 40%:
„Die Impfeffektivität für die Altersgruppe 12-17 Jahre wird derzeit noch nicht berichtet. Aufgrund der in dieser Altersgruppe noch niedrigen Impfquote und gleichzeitig geringen Anzahl von Impfdurchbrüchen besteht hier ein erhöhtes Verzerrungsrisiko.“
In der israelischen Studie „Green Pass and COVID-19 Vaccine Booster Shots in Israel – A More ‚Realistic‘ Empirical Assessment Analyzing the National Airport Data“ findet man in der Tabelle 1 in der ersten Zeile eine Impfeffektivität von minus 146%. Die Gruppe der Geimpften ist auch hier kleiner als die der Ungeimpften.
Statement von Reinhard Seyfarth
Da ich kein Medizinstatistiker bin, fordere ich zum offenen wissenschaftlichen Dialog über die von mir angeführten Sachverhalte auf. Prof. David Spiegelhalter, der für seine Verdienste um die englische Medizinstatistik zum Ritter geschlagen worden ist, fasst den Umgang mit Statistik in drei wesentlichen Punkten zusammen:
- Offenlegung der Daten
- Ehrlichkeit, also berechnen und interpretieren ohne Agenda
- Nachvollziehbarkeit und Transparenz.
Mir scheint, dass der Umgang des RKI mit den Pandemiezahlen hier großen Nachholbedarf hat. Es geht um die Gesundheit des ganzen Volkes und insbesondere der Älteren und der Kinder.
Wie können vernunftbegabte Abgeordnete auf Basis solcher Statistik-Kapriolen eine allgemeine Impfpflicht beschließen wollen?
Die Farrington-Formel
Mit:
VE = Impfeffektivität;
PCV = Anteil der Geimpften an den (schwer) Erkrankten
PPV = Anteil der Geimpften an der untersuchten Grundgesamtheit
lautet die Formel nach Farrington:
VE = 1 – PCV/(1- PCV) * (1-PPV)/PPV
Korrekturhinweis (6.12.): In die Farrington-Formel hatte sich im hinteren Teil ein Fehler in der Klammersetzung eingeschlichen. Den habe ich korrigiert.
